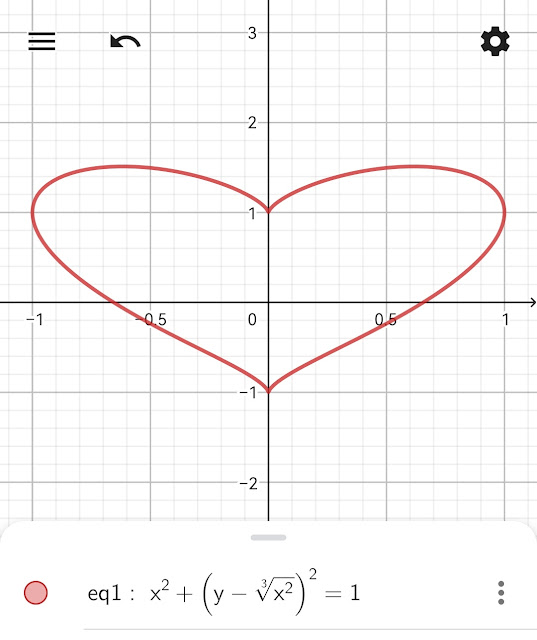
Βρείτε το μήκος x της πλευράς του τετραγώνου.
Τρίτη 23 Απριλίου 2024
Δευτέρα 8 Απριλίου 2024
"Αναμνήσεις συμμετρίας"
Το βιβλίο
"Αναμνήσεις Συμμετρίας" του μαθηματικού Ανδρέα Λύκου είναι «μία
μυθιστορηματική περιήγηση στο έργο του χαράκτη Μ. Κ. Έσερ», όπως το
χαρακτηρίζει ο ίδιος ο συγγραφέας. Ο Ανδρέας Λύκος κατάφερε να ισορροπήσει με
αξιοθαύμαστο τρόπο στην αφήγηση της ιστορίας του διαφορετικούς και σύνθετους
κόσμους: την πολυδιάστατη ομορφιά της τέχνης του Ολλανδού χαράκτη Έσερ, τη
μαθηματική επιστήμη και την αναζήτηση της συμμετρίας, με την παλαιότερη από τις
ανθρώπινες περιπέτειες, εκείνη του έρωτα και της ένωσης των ανθρώπων.
Βασικοί ήρωες
αυτού του επιστολογραφικού μυθιστορήματος, με τις υποκειμενικές αφηγήσεις των
ηρώων, είναι η Ραφαέλα, φοιτήτρια Ιστορίας της Τέχνης, και ο Θωμάς,
διδακτορικός φοιτητής μαθηματικών, οι οποίοι παρατηρούν, ο ένας στη Ρώμη και ο
άλλος στη Χάγη, το ίδιο έργο του χαράκτη Μ.Κ. Έσερ, την περίφημη
λιθογραφία «Πινακοθήκη» (1956). Ο πίνακας που κοιτούν
γοητευμένοι οι δύο ήρωες σε διαφορετικές τοποθεσίες αποτελεί και το όχημα που
θα τους μεταφέρει, με απρόβλεπτο τρόπο, στην ίδια πόλη. Το Ατράνι, μια μικρή
ιταλική πόλη, που έχει απεικονίσει πολλές φορές ο Έσερ στα χαρακτικά του, θα
γίνει ο τόπος στον οποίο θα βιώσουν ένα πρωτόγνωρο συναίσθημα, εκείνο της
βιωματικής προσέγγισης ενός έργου τέχνης. Εκεί θα γνωρίσουν τους
"ανέφικτους κόσμους" του, καθώς και τα έργα του που διέπονται από
τους κανόνες της συμμετρίας. Οι
ήρωες του βιβλίου περπατούν δίπλα στους «Καταρράκτες»,
τους «Βυθισμένους Καθεδρικούς ναούς» και στις αδύνατες
κατασκευές του χαράκτη, προσπερνώντας παράξενα συμμετρικά πτηνά,
σαύρες ή περίτεχνα γεωμετρικά σχήματα. Ξεναγός τους θα είναι ο ίδιος ο
χαράκτης.
 |
| Το έργο «Πινακοθήκη» (1956) του Μ.Κ. Έσερ |
Πώς, όμως, μία
ιστορία στα Γιάννενα του δευτέρου παγκοσμίου πολέμου και ένας έλληνας
μαθηματικός του 20ού αιώνα θα επηρεάσουν τη μετέπειτα ζωή τους; Μία επιδέξια
ακροβασία ανάμεσα στο υπαρκτό και το νοητό, μία ευτυχισμένη συνάντηση του
ορθολογισμού με το συναίσθημα, μία ερωτική περιπέτεια όπου πρωταγωνιστούν τα
μαθηματικά και η τέχνη.
Μπορείτε να
διαβάσετε το βιβλίο σε ηλεκτρονική μορφή, καθώς διατίθεται δωρεάν εδώ.
Δευτέρα 11 Μαρτίου 2024
"Ιστορίες Μαθηματικής Φαντασίας"
Έντεκα διηγήματα από τον εξωτικό κόσμο των μαθηματικών
Τα μαθηματικά ως επιστήμη αποκαλύπτουν τα ορθολογικά θεμέλια του κόσμου μας και, παράλληλα, δίνουν έρεισμα για φιλοσοφικές προεκτάσεις. Ήταν επόμενο να γοητεύσουν τον Ζήνωνα, τον Άμποτ και τον Μπόρχες, δίνοντας έμπνευση και μέθοδο για ιστορίες και πειράματα σκέψης που εξετάζουν τον κόσμο μας από το μηδέν ως το άπειρο, από τον άνθρωπο ως το σύμπαν.
Χιούμορ και δράμα, ευφάνταστες αφηγήσεις και νοητικές αναζητήσεις. Τα διηγήματα που φιλοξενούνται σ' αυτή την ανθολογία μάς προσφέρουν μαθηματικά λογοπαίγνια, τοπολογικούς λαβύρινθους, γεωμετρικές περιπέτειες: ένας άνθρωπος που παγιδεύεται σε μια χώρα δύο διαστάσεων... ένας φοιτητής που πρέπει να βρει τρόπο να ξεφύγει από μια συμφωνία με το διάβολο... ένας πόλεμος με εξωγήινους που διεξάγεται αποκλειστικά με την απόδειξη μαθηματικών θεωρημάτων... ένα τρένο που εξαφανίζεται από τις ράγες του... και τι κάνουμε όταν χαλάσει ο υπολογιστής του διαστημοπλοίου μας...
Γράφουν μερικοί από τους κορυφαίους συγγραφείς του είδους: Άρθουρ Κλαρκ, Λάρι Νίβεν, Γκρέγκορι Μπένφορντ, Ρόμπερτ Χάινλαϊν, Ρούντι Ράκερ, Γκρεγκ Ίγκαν, Μάρτιν Γκάρντνερ, Άρμιν Γιόζεφ Ντόιτς, Χένρι Γκρος, Τζορτζ Ζιμπρόφσκι και Άλφρεντ Μπέστερ.
Επιλογή κειμένων και μετάφραση: Χριστόδουλος Λιθαρής.
Δευτέρα 4 Μαρτίου 2024
Μαθηματικός γρίφος: Διατεταγμένες τετράδες
Να βρείτε όλες τις διατεταγμένες τετράδες \( (x, y, p, q) \) θετικών ακεραίων, όπου \( p, q \) πρώτοι, τέτοιες, ώστε \( \big(\frac{1}{x}\big)^2 + \big(\frac{1}{y}\big)^2 = \frac{1}{pq} \)
Ευχαριστώ τον συνάδελφο Μιχάλη Ζαρτούλα, που μου έστειλε τον γρίφο!
Τετάρτη 14 Φεβρουαρίου 2024
Ο Άγιος Βαλεντίνος πάει Λύκειο...
Κάθε γραμμή στο επίπεδο είναι μια γεωμετρική οντότητα, η οποία "συνοδεύεται" και από τη δική της εξίσωση, που είναι η αλγεβρική της "υπόσταση". Αυτή είναι η βασική σύνδεση της Άλγεβρας με τη Γεωμετρία. Για παράδειγμα, η εξίσωση της μορφής \( αx + βy = γ \), με \( α \neq 0 \) ή \( β \neq 0 \) παριστάνει ευθεία. Η εξίσωση της μορφής \( x^2 + y^2 = ρ^2 \) παριστάνει κύκλο.
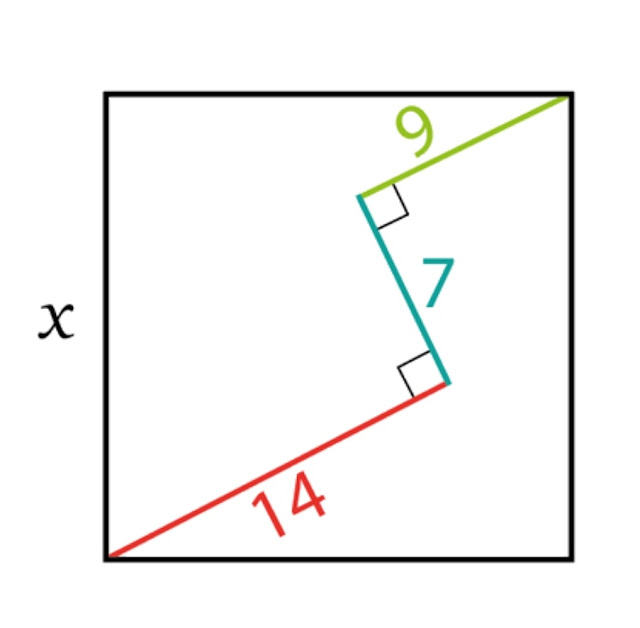
Αν θέλεις να ζωγραφίσεις μία καρδιά, μπορείς να χρησιμοποιήσεις μία από τις παρακάτω εξισώσεις. Η πρώτη καμπύλη (πάνω αριστερά) ονομάζεται καρδιοειδής καμπύλη.
 |
| Πηγή εικόνας: Wolfram MathWorld |
Στο σχολείο μας, είπαμε να αφήσουμε για μια στιγμή την ευθεία και τον κύκλο των Μαθηματικών Κατεύθυνσης της Β΄ και να σχεδιάσουμε, χρησιμοποιώντας το Geogebra, τη δική μας καρδιά...
Κυριακή 11 Φεβρουαρίου 2024
"Σε φάση μετάβασης"
Ιστορίες (συν)εργασίας στην τάξη των γυμνασιακών μαθηματικών
Δίχως αμφιβολία το
Γυμνάσιο είναι μια από τις πιο σημαντικές, ίσως η σημαντικότερη, βαθμίδα της
εκπαίδευσης. Άλλωστε και ηλικιακά αντιστοιχεί στο πέρασμα στην εφηβεία, ένα
πέρασμα, που όπως λένε οι επαΐοντες, μπορεί να καθορίσει σε μεγάλο βαθμό όλη
την υπόλοιπη ζωή μας... Για τα μαθηματικά πάντως, είναι βέβαιο πως πρόκειται
για ένα κρίσιμο σημείο καμπής.
...Δύσκολο έργο για ένα πιτσιρίκι –που νιώθει τα μέλη του να μεγαλώνουν
ανεξέλεγκτα, τους χυμούς και τις ορμόνες να κάνουν μέσα στο σώμα του γιορτή– να
κατανοήσει τις πρώτες ανατροπές σ’ αυτά που ως τότε ήταν οι ακλόνητες
(μαθηματικές) πεποιθήσεις του. Δύσκολο έργο όμως και για το δάσκαλο, που
μπαίνοντας μέσα στην τάξη έχει να αντιμετωπίσει «ένα μελίσσι που ορμά στη
γύρη... και άλλοτε του αφήνει μια γλυκιά γεύση στα χείλη κι άλλοτε ένα ηχηρό
βουητό στα μηνίγγια».
Πέρα όμως από τις δυσκολίες που πρέπει να είναι έτοιμος και πρόθυμος να
αντιμετωπίσει κάποιος που επέλεξε να γίνει δάσκαλος, υπάρχουν κι άλλες,
απροσδόκητες και πολύ πιο σύνθετες: η «πατρομητρότης» που βασανίζει τη
γυμνασιακή βαθμίδα όταν, θεωρώντας πως το βλαστάρι της δικαιούται τον
«καλυτερότερο» βαθμό, προσλαμβάνει ειδικούς και επεμβαίνει στη διδασκαλία. η
πολιτεία με τα ακατάλληλα, απηρχαιωμένα βιβλία και προγράμματά της. η δυσπιστία
του μέσου πολίτη –που ενίοτε είναι και συνάδελφος άλλης ειδικότητας, για να μην
πω της ίδιας– απέναντι στα μαθηματικά...
Τούτο το υπέροχο μπουκέτο από εμπειρίες, πρωτοβουλίες, απογοητεύσεις και
θριάμβους, ζωντανό, γλαφυρό και μεθοδικό, μας ταξιδεύει στον φριχτό και υπέροχο
συνάμα κόσμο της εκπαίδευσης. Μέσα από τις σελίδες του ανακαλύπτουμε ιστορίες
που όλοι ζήσαμε και που τις ζωγράφισε για χάρη μας, νομίζοντας πως φωτογραφίζει
μονάχα τον εαυτό της, η μοναδική, υπέροχη Κατερίνα Καλφοπούλου.
(Το κείμενο είναι του Τεύκρου Μιχαηλίδη, από την παρουσίαση στο οπισθόφυλλο του βιβλίου)
Πέμπτη 1 Φεβρουαρίου 2024
Κουίζ σε πίνακα 3x3
Κάθε αριθμός παριστάνει το άθροισμα σε κάθε γραμμή ή σε κάθε στήλη αντίστοιχα. Ποιοι αριθμοί πρέπει να αντικαταστήσουν το κόκκινο και το γκρι ερωτηματικό;
Σάββατο 27 Ιανουαρίου 2024
Τα μαθηματικά του Louis de Funès: 66+99=?
Σαν σήμερα το 1983, έφυγε από τη ζωή ο Λουί ντε Φυνές, ένας από τους σημαντικότερους κωμικούς ηθοποιούς στην ιστορία του γαλλικού κινηματογράφου. Ο συνάδελφος και αναγνώστης του μπλογκ, Carlo de Grandi, μου έστειλε αυτή την αξέχαστη φωτογραφία με τις... μαθηματικές πράξεις του Λουί ντε Φυνές.
Κυριακή 21 Ιανουαρίου 2024
Γρίφος: Τα ορθογώνια
Πηγή: Τελικός Διαγωνισμός Μαθηματικών Α΄ Γυμνασίου 2023-2024 "Ο ΙΠΠΑΡΧΟΣ", Ελληνική Μαθηματική Εταιρεία - Παράρτημα Δωδεκανήσου, 20/01/2024

%20cubes.png)